The Assumptions for Triple Difference
- Karl 曹
- Jul 22, 2022
- 2 min read
Triple difference is an extended version of Difference-in-Difference, and it also requires common trend assumption, but according to
Andreas Olden, Jarle Møen, The triple difference estimator, The Econometrics Journal, 2022;, utac010, https://doi.org/10.1093/ectj/utac010
triple difference only needs one common trend assumption. This blog will explain above paper.
Here we assume that we have two groups, treatment group (T) and control group (C). In addition each group has two sub-groups, gruop A and gruop B.
The treatment of course has been implemented on group T. However, different from usual DiD situation, treatment only influences sub-group B in gruop T, and the sub-group A in T is not treated directly (here we cannot exclude the possibility that B in T has spillover effect on A in T). What we are interested in is the treatment effect on B in group T, we name it as delta.
At first we may take A in T as control group for B in T, but there maybe some spillover effect for treatment. Meanwhile if we only take B in C as control group, even though some covariates have been controled, group C and T may still have some difference in their developing trend. Therefore, we should introduce C and sub-group A simultaneously.
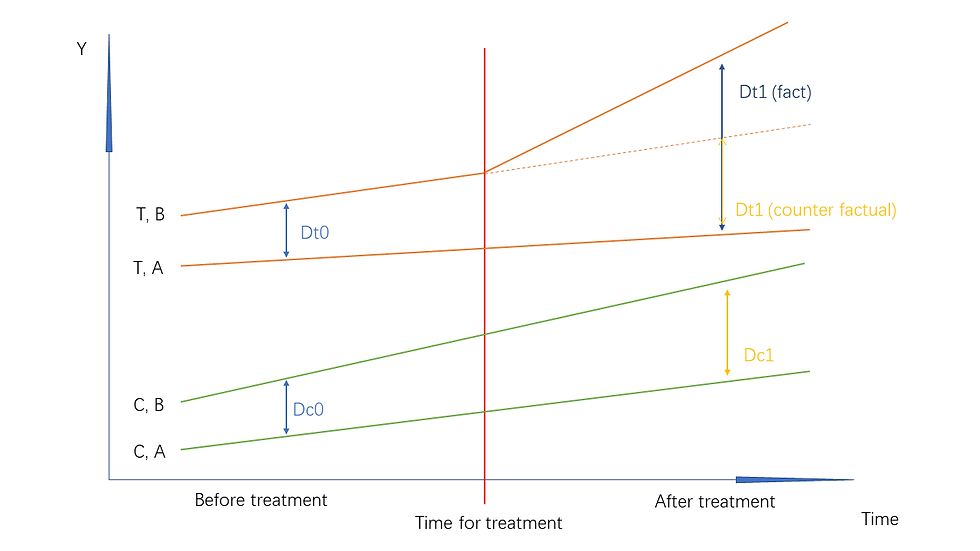
Here we assume the difference between A and B in T over time would be the same as difference between A and B in C over time, if there were no treatment on T. On the figure above that is:
Dt0 = Dc0 and Dt1(counter factual) = Dc1
=>
Dt1(counter factual) - Dt0 = Dc1 - Dc0.
And what we interested, delta, is estimated as:
delta = [Dt1(fact) - Dt0] - [Dc1 - Dc0]
This is similar to an usually used DiD estimator.
Delta will have a causal interpretation if our assumption holds, that is :
delta = [Dt1(fact) - Dt0] - [Dt1(counter factual) - Dt0] = Dt1(fact) - Dt1(counter factual)
In summary, triple difference only requires one common trend assumption: the difference between A and B in group T has the same trend as the difference between A and B in group C in the absence of treatment.



Comments